2020 Waterloo CCC Junior Problem Solution

Hey There!

Hope you are doing well. This is an explained solution of the problems on Programming contest (Junior Category) on Canadian Computing Competition 2020. The solutions and explanations are made by keeping in mind that this is your first participation in a programming contest. I would suggest you to try to code first after reading the explanation and before seeing the solution code. Keep practicing and solving the problems. Happy Coding!

Problem J1: Dogs Treats

This is a pretty straightforward problem. Let’s understand the problem first then we will move into the solution. We need to find whether our dog Barley is happy or sad based on the formula given in the Problem description. 

1  S + 2  M + 3  L

Here, 

S = Small Treat

M = Medium Treat

L = Large Treat

Now, using the formula, we will get a happiness score. we have to print happy if the happiness score is 10 or greater, otherwise sad.

You can find more knowledge explanation for Data Structures in Python

‍

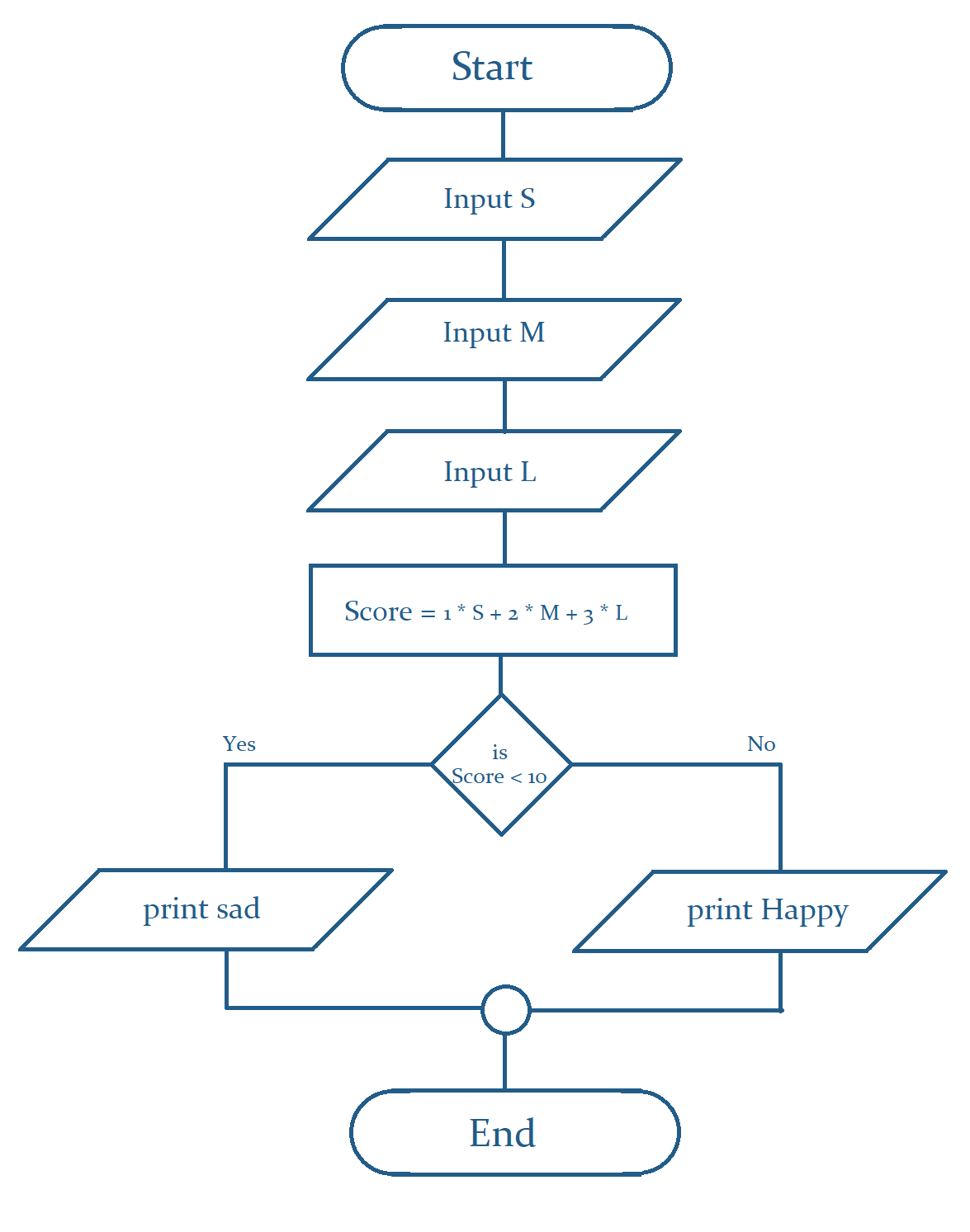
So, before going to code, we have to take a look at the input and output specifications. Remember, we need to write our code in such a way that we can enter our values of Small, Medium, and Large treat exactly as the sample input given in the problem. Also, we have to print our output happy or sad exactly as given in the sample output. The sample output is case-sensitive so we need to be careful about that.

Time complexity:

Since we are not using any for loop here and for every case of input, we have to perform similar task, we can say that the time complexity of this problem is constant or O(1). 

S = int(input())
M = int(input())
L = int(input())
 
score = 1 * S + 2 * M + 3 * L
 
if score < 10:
    print("sad")
else:
    print("happy")

‍

Problem J2: Epidemiology

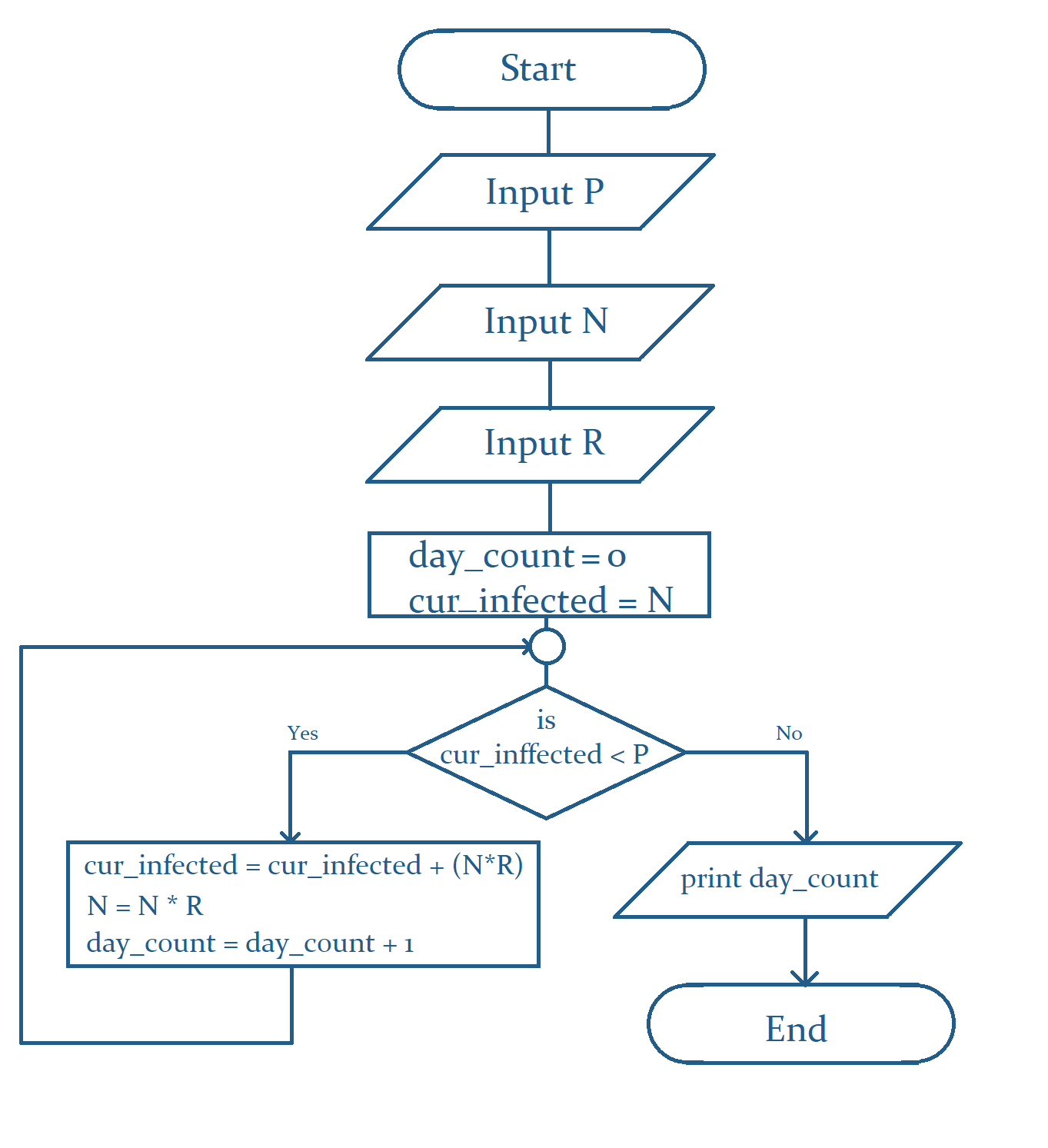
Our second problem is about making a simple model to analyze the spread of disease. We will be given 3 pieces of information. First, we will be given P. We want to determine how many days it will take to have more than P people get infected. Next, we will be given N, the number of people at the beginning (Day 0). Finally, we will be given R which is the exact number of people will get infected by a person who has a disease. We want to calculate how long it will take for more than P persons to become infected.

While solving this problem, it is necessary to understand all the conditions in the problem. To start with, a person can only be infected once in this simple model. We also need to understand the value of R. R is the “exact” number of people who will get infected by a single infected person but only on the next day. That means, if a person gets infected on day 2, he will infect R number of people on day 3, but he will not make any other people get infected on upcoming days. Don’t worry, you will get a clear idea after we analyze our first sample input.

In Sample Input 1, there is only 1 person infected on Day 0. Since the value of R is 5, our infected person will infect 5 other people on Day 1. On the following day, only those people will spread the diseases who got infected in the previous day. So, 5  5 = 25 new people will get infected. Note that, the person from day 1 is not spreading the disease anymore.

Since we understand the conditions of this model, let’s look into the flowchart before going to the coding section. 

In the flowchart, we took a variable cur_infected which is representing the total number of infected people. We are using a loop where each iteration is calculating the number of infected people in a day. We are also updating the value of N which is indicating how many people are newly infected and able to spread diseases in the next day.

Time Complexity:

There is a loop in this code. In the worst case, the value of R and N will be 1, then only 1 person will get infected each day. In that case, it will take P - 1 days, which means the loop will run P - 1 times. 

If P = n

Then,

Time Complexity = O(n-1)  O(n)

‍

‍

P = int(input())
N = int(input())
R = int(input())
day_count = 0
current_infected = N
while (current_infected <= P):
    current_infected += N*R
    N *= R    
    day_count += 1
print(day_count)

‍‍‍

Problem J3: Art

Our third problem is a little bit tricky and required some thinking. But once you get the main idea, it will be a piece of cake for you. In this problem, Mahima is going to flick some paint on the canvas. We need to find the smallest possible frame so that all the paint drops are inside the frame. In this problem, we are considering the canvas as an XY plane, where (0,0) coordinates represent the bottom-left corner of the canvas. Let’s look at the diagram below for a clear idea.

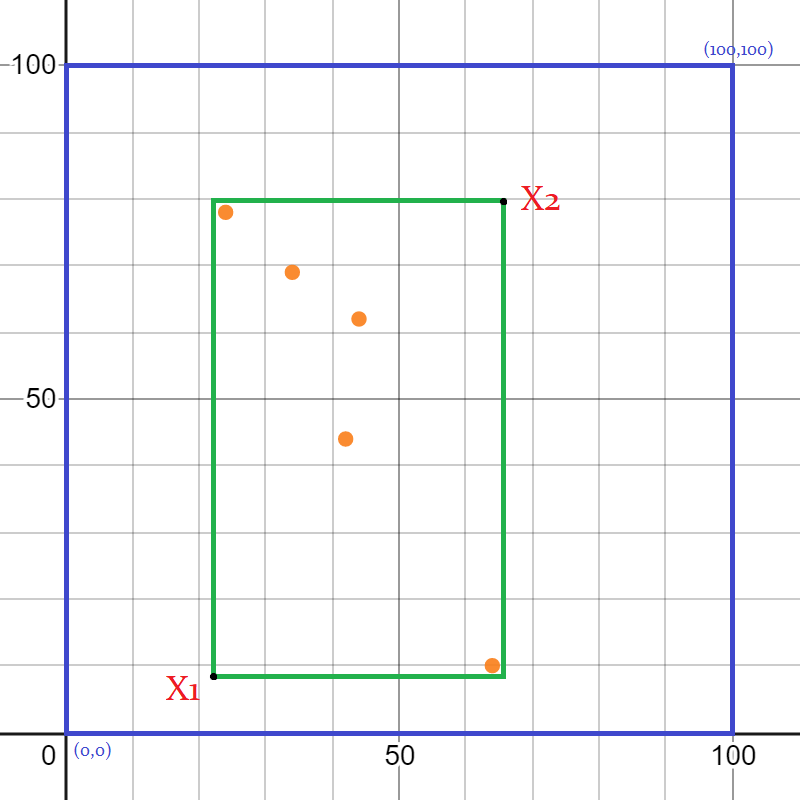
In the diagram, the blue square is our canvas for this problem, orange dots are the drop of paint, the green square is the smallest possible rectangular frame. We need to print the coordinates of the bottom left corner X1 and the top right corner X2 of the green square for this problem.

So, we are given the coordinates of the paint drops and now we know what we have to print. You may already guess how we will find out X1and X2 but if not then do not worry.

If we look carefully, we can see that among the coordinates of all paint drops, the “lowest x coordinate - 1” is representing the left side of the green frame, and the “highest x coordinate - 1” is representing the right side of the green frame. We are subtracting 1 because it was told that points on the frame are not considered inside the frame.  Similarly,  the “lowest y coordinate + 1” is representing the bottom side of the green frame and the “highest y coordinate + 1” is representing the top side of the green frame. We are adding 1 because it was told that points on the frame are not considered inside the frame.

Therefore, we need to find out the X1and X2 by following,

X1= (min(x)-1,min(y)-1) 

X2= (max(x)+1,max(y)+1)

Time Complexity:

Our code consists of one for loop which will iterate N times. So, the time complexity is O(n).

N = int(input())
min_X, min_Y = 101, 101 #100 is the maximum coordinate in the canvas
max_X, max_Y = -1, -1   #0 is the minimum coordinate in the canvas
for i in range(N):
    cords = input().split(',')
 
    #Finding if the current input contain max or min values of x and y
 
    if int(cords[0]) < min_X: 
        min_X = int(cords[0])
    if int(cords[0]) > max_X:
        max_X = int(cords[0])
    if int(cords[1]) < min_Y:
        min_Y = int(cords[1])
    if int(cords[1]) > max_Y:
        max_Y = int(cords[1])

‍

Problem J4: Cyclic Shifts

This problem is also pretty straightforward if you can understand how to shift a string cyclicly. We will be given a text and a string. We have to find out if the string or the cyclic shifts of the string is a substring of the given text. We can shift a string cyclicly in various ways in python. We are going to show by slicing the string.

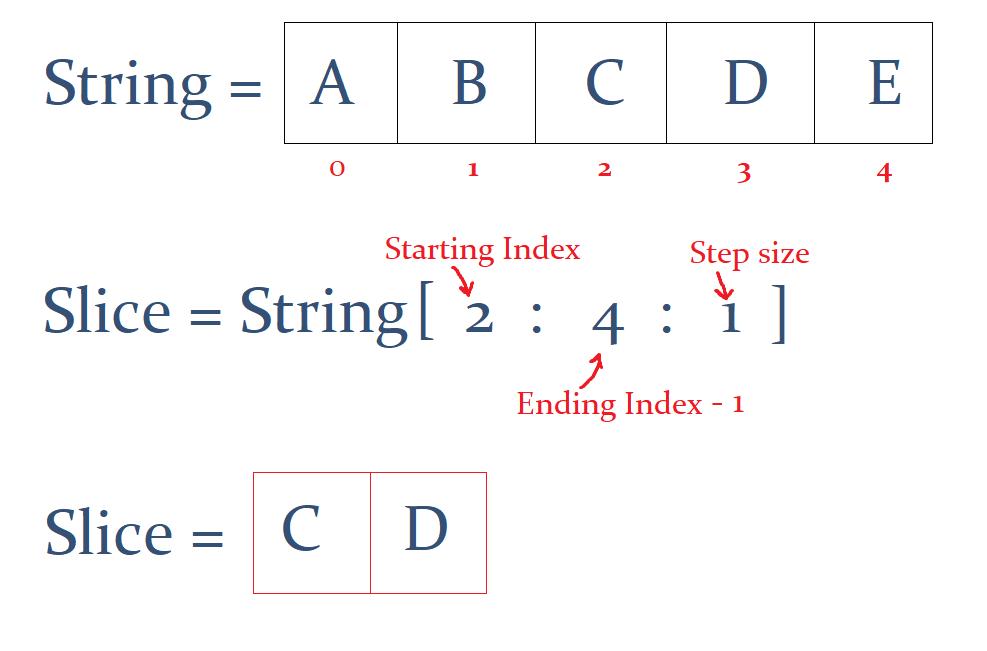
Slicing in python means obtaining a substring from a string by slicing it from starting index to ending index - 1. We can also use step size. Look at the picture below for further clarification.

To shift a string for once, we have to put the first character to the end of the string. We can do it by slicing the string from index 1 to its end and then adding the first character at the tail of the string. The following code snippet will give you a clear idea.

We can reduce 3 lines of code into 1 line. Then it will be,

String = String[1:] + String[0]

So, we learned how to shift a string cyclicly. Now, we have to see if the string is a substring of the given text. If not, then we will shift it again and check if that is a substring or not. We will do it till the length of string times. If we find the substring then we will print yes otherwise no. We will use a boolean not_found to check if the text does not contain a cyclic shift of the string.

Time Complexity:

Substring in String takes O(nm) in the worst case where m = length of string and n = length of substring we are looking for. We need to do this O(nm) search n times in the for loop. 

So, the Total time complexity would beO(n2m) in the worst case.

T = input()
string = input()
not_found = True
for i in range(len(string)):
    if string in T:
        not_found = False
        print('yes')
        break
    string = string[1:] + string[0]
 
if not_found:
    print('no')

‍

Problem J5/S2: Escape Room

This problem is a bit tricky. You need to understand quite a few things before proceeding. First of all, you need to know about Breadth First Search (BFS) and Depth First Search (DFS). You can go to the following link for further clarification about BFS and DFS.

BFS and DFS

Here, we will use DFS to solve this problem. As you can see the room is an MxN grid where 1  M, N  1000 and (1,1) is our starting point and (M, N) is our ending point.  Each cell in the grid contains an int x. The factorization of x will be the cell we can go from that cell to (factor1,factor2). For example, if grid(1,1) contains 4, then we can go from (1,1) to (1,4) or (2,2) or (4,1). Please note that we can only go to the cell which is actually in the grid. For clarification, if we are having a 3x3 grid, we can not go (1,4) or (4,1) grid.

To solve this problem, at first, we need to define a 2-dimensional vector and boolean array. In C++, vectors are sequence containers that represent arrays that can change size during execution. We will define (1000000 + 10) lengths for both of them. We are doing it because the maximum size of the room can have 1000x1000 which means there can be a maximum of 1000000 cells. We are taking 10 extra to avoid any kind of error.

Now, we will take input and store it in the room vector. In the input, room[r][c] contains the integer in the r-th row and c-th column. If we can reach any cell (r,c) with rc = x , set visited[x] = True, otherwise False. If, visited[x] is True then we can say that visited[room[r][c]] is true for all (r,c) cells with  rc = x. As a result, we obtain a directed graph with vertices 1 to 1000000 and a directed edge from x room[r][c]. Now, all we have to do is check if there is a path from 1 to N*M whenever rc = x.

Now, we will begin our DFS algorithm for vertex 1 and mark all of the vertices as visited in the boolean array, If we set visited[M*N] is True then there is a path exist from 1 to cell MxN.  Then we will print yes and exit. If we cross our boundary MxN then we will return. These two cases will be our base condition for the DFS algorithm. Otherwise, we will set visited[x] = True and continue our search. If there is no path from cell 1 to MxN that means, then the DFS function will finish running and then we will print no.

Time Complexity:

There are two for loops for taking input, which will have a time complexity of O(MN). The time complexity of DFS if the entire tree is traversed is O(V) where V is the number of Nodes. We have a graph with MxN nodes. So, Total time complexity of this code will be O(MN+MN)  O(MN)

#include <bits/stdc++.h>
 
using namespace std;
 
// Initializing the vector and arrays
int M, N;  
vector<int> room[1000005];
bool visited[1000005];
 
void dfs(int x) {
    // Checking if the cell is already visited or not
    if (visited[x]) {
        return;
    }
    // Checking if we have reached exit or not
    if (x == N * M) {
        cout << "yes" << endl;
        // Terminating
        exit(0);
    }
    // Setting the cell as visited
    visited[x] = 1;
    // Continuing the search
    for (int& t : room[x]) {
        dfs(t);
    }
}
 
int main() {
    // Taking input
    cin >> M >> N;
    for (int i = 1; i <= M; i++) {
        for (int j = 1; j <= N; j++) {
            int x;
            cin >> x;
            room[i * j].push_back(x);
        }
    }
    dfs(1);
    cout << "no" << endl;
}
 

‍

‍

‍

Related topics: High School Math and Coding Contest: Complete Guide for Waterloo CEMC Contests

How to get into a top-tier university?

‍

‍