2022 Waterloo CCC Senior Problem Solution

In this tutorial, we are going to look at an explained solution of the problems in the Programming contest (Senior Category) on Canadian Computing Competition 2022. The solutions and explanations are made by keeping in mind that this is your first participation in a programming contest. I would suggest you try to code first after reading the explanation and before seeing the solution code. Keep practicing and solving the problems. Happy Coding!

Problem S1: Good Fours and Good Fives Statement:

You are given a number. You have to print the number of ways, this number can be represented using a sum of fours and fives. Number of fours or fives must be different in each way.

Idea:

If we take k number of fives, can you say whether we can make sum using any number of fours? We can make desire sum if the remaining value (that is n-k*5) is divisible by 4. So, one optimal way is to run a loop from 0 to n, and check for every possible number of fives, if it’s possible to make sum equal to n just increment your answer by 1.

Complexity: O(n) here n can be upto 1e6. As we are iterating from 0 to n;

‍Flowchart:

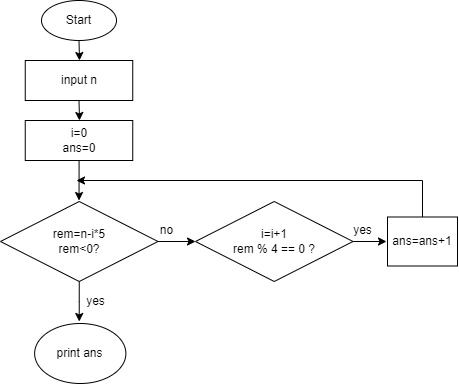
Code: C++

#include <bits/stdc++.h>
using namespace std; 
int main()
{
    int n; cin>>n;
    int ans=0;
    for(int i=0;i<=1000000;i++)
    {
        int total=i*5; 
        int rem=n-total;
        if(rem>=0 and rem%4==0) ans++; 
    }
    cout<<ans<<endl; 
}

‍

Problem S2: Good Groups Statement:

You are given some number of groups. Each group consists of three members. There are two types of constraints:

1. given two names, they must be in the same group
2. given two names, they must be in the different group.

Now you have to count number of groups that violate one of these two constraints.

Idea:

For each type (i) and type (ii) constraints, you have to check whether they are in the same group or not. How can you determine the two members are in same group? We can use a disjoint set union to check it. Disjoint set join stores the connected components and all these connected components have the same parent.

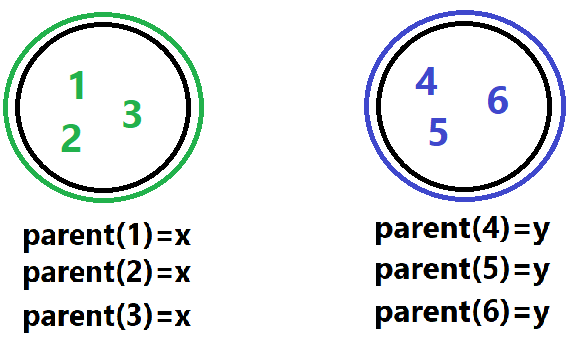
So for each two members, if their parents are same for type (ii) constraint that means this constraint is violated. We will increment our answer by 1. Can you do the same for type (i)? I think so. Now, the important part is to store the names of each member. One possible way is to store the hash value of each name. Instead of using hash value, we can use STL map, that takes log(n) time to store a name and it’s fine as we have enough time to execute all test cases.

Complexity: O(nlogn) as there are n names, each takes logn time to store.

Flowchart:

‍

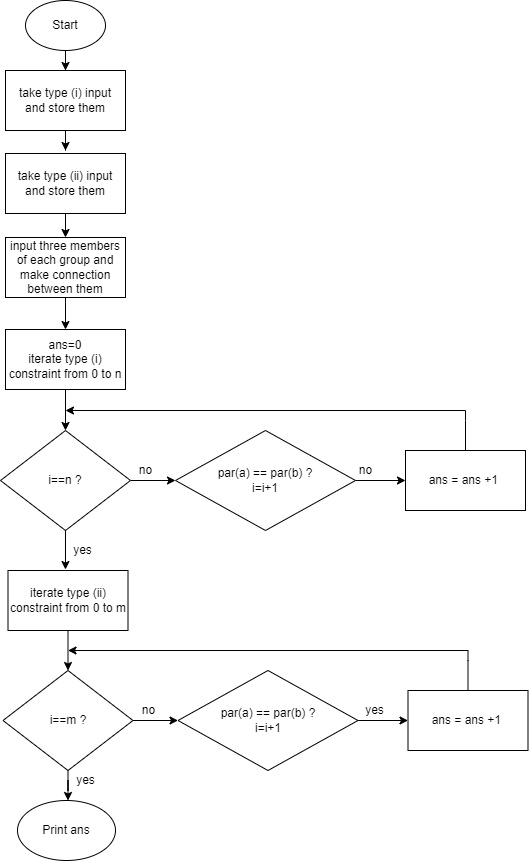
Code: C++

#include <bits/stdc++.h>
using namespace std;
const int mx=3e6+9;   
int par[mx]; 
map<string,int> mm; 
int findp(int x)
{
     if(x==par[x]) return x;
     return par[x]=findp(par[x]);
}
void  join(string &a, string &b)
{
     int f=findp(mm[a]);
     int s=findp(mm[b]);
     par[f]=s; 
}
bool check(string &a, string &b)
{
     int f=findp(mm[a]);
     int s=findp(mm[b]);
     if(f==s) return 0; 
     return 1; 
}
int main()
{
     for(int i=1;i<=1000000;i++) par[i]=i;
     int cnt=1;
     int  n; cin>>n; 
     vector<pair<string,string> > v(n);
     for(auto &x: v) 
     {
          cin>>x.first>>x.second; 
          if(mm[x.first]==0) mm[x.first]=cnt++; 
          if(mm[x.second]==0) mm[x.second]=cnt++;
     }
     int m; cin>>m; 
     vector<pair<string,string> >v1(m);
     for(auto &x: v1) 
     {
          cin>>x.first>>x.second;
          if(mm[x.first]==0) mm[x.first]=cnt++; 
          if(mm[x.second]==0) mm[x.second]=cnt++;
     }
     int g ; cin>>g;
     while(g--)
     {
          string a,b,c; cin>>a>>b>>c;
          if(mm[a]==0) mm[a]=cnt++; 
          if(mm[b]==0) mm[b]=cnt++;
          if(mm[c]==0) mm[c]=cnt++; 
          join(a,b);
          join(b,c);
     }
     int ans=0; 
     for(auto x: v)
     {
          ans+=check(x.first,x.second);
     }
     for(auto x: v1) 
     {
          if(check(x.first,x.second)==0) ans++; 
     }
     cout<<ans<<endl;
}

‍

Problem S3: Good Samples Statement:

You are given a series of notes. Each note is an integer. You can select any non-empty sequence of consecutive notes without any repetition that means all notes in a selected sequence must be distinct. This selected sequence is called sample. You have to construct a series of notes of length n where each note will be between 1 to m (inclusive) and total number of sample will be exactly k. can you do this?

Idea:

Let’s consider this sequence:

5

1

2

Each element in this sequence is distinct. How many new samples will be created if I add a distinct number at 4th index of this sequence?

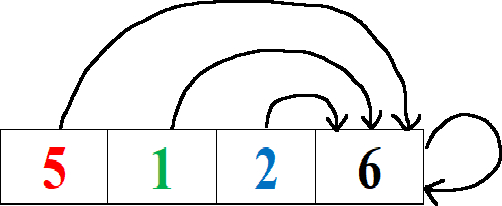
Here we can see, 4 new samples will be created. They are [5,1,2,6], [1,2,6], [2,6], [6]. So, If I want to add another distinct number at 5th index, another 5 new samples will be created. But if I add a number that is not distinct, how many new samples will be added? Let’s see the below figure:

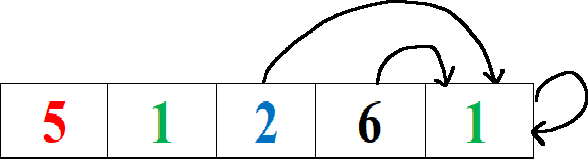
Only 3 samples are added. They are [2,6,1],[6,1],[1]. So, here’s the conclusion:

If we add a distinct number at position k, total k new samples will be added.

If we add a non-distinct number at position k, total (k-previous position) new samples will be added. To construct a series of n numbers,

We can run a loop from 0 to n-1. To find a number for the i th index, we will make a decision whether we will select a distinct or non-distinct number by observing the remaining value of

k. After selecting number, store it to a container and total number of new samples will be subtracted from k. Outside the loop, we can simply check the value of k. if value of k is zero, that means, we have successfully created our desired series. Just print all stored values. Otherwise print -1.

Complexity: O(n) where n is the length of series.

Code: C++

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mx=3e6+9;   
int main()
{
     ll n,m,k; 
     cin>>n>>m>>k; ; 
     vector<ll> ans; 
     for(ll i=0;i<n;i++)
     {
          ll rem=n-i-1; 
          ll cur=min(k-rem,m);
          if(cur<=0) break;  
          ll val; 
          if(cur>i)
          {
               val=min(m,i+1);
               cur=val; 
          }
          else val=ans[i-cur]; 
          ans.push_back(val);
          k=k-cur; 
     }
     if(k==0 and (ll)ans.size()==n)
     {
          for(auto x: ans) cout<<x<<' '; 
          cout<<endl; 
     }
     else cout<<-1<<endl;
}

Problem S4: Good Triplets Statement:

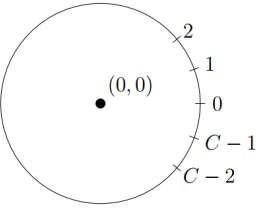
A circle is given with (0,0) center. The circumference of the circle is C. So there can be total C integer points on the boundary of the circle. Total n points are drawn. The location of the points on the circle is the counter-clockwise arc length from the right-most point of the circle. Multiple points can be drawn at the same location. Your task is to calculate the number of ways to select three points in such a way that if we create a triangle using this three points, circle’s center will be strictly inside the triangle.

Idea:

We will follow a different approach to solve this. How many ways are there to select 3 points from n?

It’s = n*(n-1)*(n-2)/6. But we can’t include all these ways to our answer as some ways won’t make a triangle that satisfy conditions. We must subtract the number of ways to select 3 points from n that don’t satisfy conditions. So,

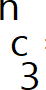
ans = n*(n-1)*(n-2)/6 – (number of ways that don’t meet the conditions)

Now, our target is to calculate number of ways of select 3 points from n that don’t meet the conditions. We will iterate every points that are drawn on the circle and count how many ways are there to select another two points such that these points create a triangle that don’t meet the condition. We sum up all these ways and subtract it from

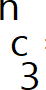
. How can we do this?

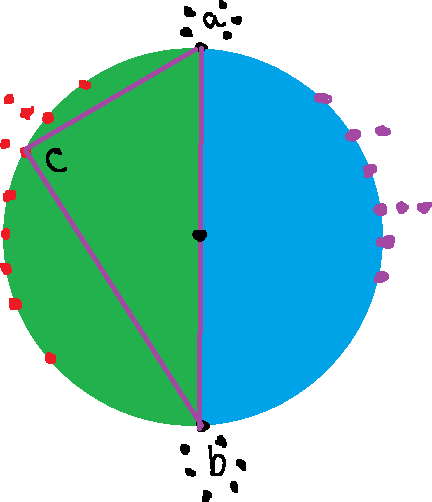
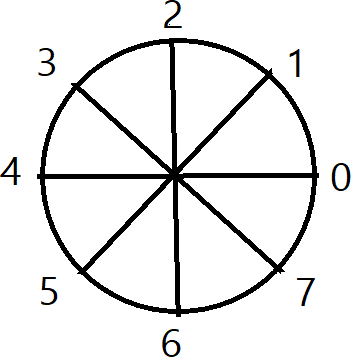
Say, we are on point a, we will find the opposite point of a and it’s b. if the circumference is C, then opposite point of a will be (a+c/2)%c. Look at the above right sided figure, the circle’s circumference is 8, so opposite point of 2 is (2+8/2)%8 =6 . For a particular point a, we will find opposite point of it (b). Calculate total number of points from a to b in counter clock-wise. we are selecting these because using any three points from these, creating triangle won’t meet

the condition as their center won’t inside the triangle. For better understanding, look at the left sided figure. There can be some cases to find all the ways from these points:

1. select a single point from a, take another two points from a to b

If number of total points at a is Ca, and number of total points from a to b is Cb then total ways = Ca * (Cb-1)*Cb/2 by combinatorics

2. select two points from a and take another one point from a to b

Total ways = Ca * (Ca-1)*Cb/2

3. select all three points from a

Total ways= Ca * (Ca-1)*(Ca-2)/6

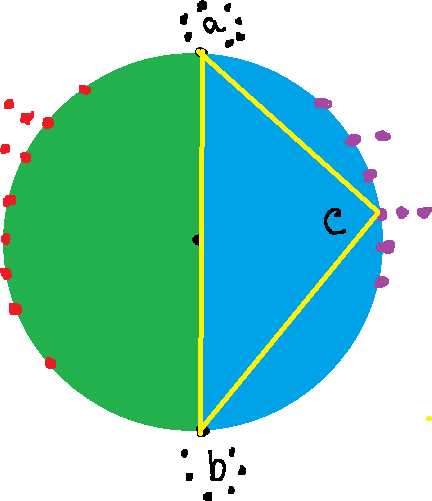
Similarly, when we are on b, its opposite point will be a. then calculate total number of points from b to a in counter clock-wise and follow the same manner when we calculated the total ways for a to b. After summing up all these ways, we will subtract this value.

Critical observation: when C is even, and we calculate ways from a to b, and ways from b to a. points that are on a and b are calculated twice.

Complexity: O(n) where n is the circumference of the circle.

Code: C++

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mx=3e6+9; 
vector<ll>sum,cnt;   
ll n,c; 
ll point(ll a, ll b)
{
     if(a<=b) 
     {
          ll d=sum[b]-(a==0?0:sum[a-1]) ; 
          return d; 
     }
     else 
     {
          ll d=sum[b]+(sum[c-1]-sum[a-1]); 
          return d; 
     }
}
int main()
{
     cin>>n>>c; 
     sum.resize(c); 
     cnt.resize(c);
     for(ll i=0;i<n;i++)
     {
          ll x; cin>>x; 
          cnt[x]++; 
     }
     sum[0]=cnt[0]; 
     for(ll i=1;i<c;i++) sum[i]=sum[i-1]+cnt[i]; 
     ll ans=n*(n-1)*(n-2)/6; 
     for(ll i=0;i<c;i++)
     {
          ll opposite=(i+c/2)%c; 
          ll tot=point(i+1,opposite);
          ans-=cnt[i]*tot*(tot-1)/2; //one
          ans-=cnt[i]*(cnt[i]-1)/2*tot; //two
          ans-=cnt[i]*(cnt[i]-1)*(cnt[i]-2)/6; //three
     }
     if(c%2==0)
     {
          for(ll i=0;i<c/2;i++)
          {
               ll opposite=i+c/2; 
               ans+=cnt[i]*(cnt[i]-1)/2*cnt[opposite]; 
               ans+=cnt[i]*cnt[opposite]*(cnt[opposite]-1)/2; 
          }
     }
     cout<<ans<<endl; 
     
}

‍

Problem S5: Good Influencers Statement:

You are given a tree of n nodes. Each node represents a student. If a student intends to write CCC, then it’s Pi will be Y, otherwise N. You can select any node with Pi=Y and pay costi dollars to force all its neighbors to write CCC. You can repeatedly select node with Pi=Y. You have to intend all students to write CCC with minimum total cost.

Idea:

Let’s introduce dynamic programming first. DP is a technique that is used in a situation where you have to calculate the same value in multiple times. Instead of calculating same value again and again, we can use DP that will store value in that state, we can simply return DP value. It minimizes our overall time complexity.

‍

A student can act as following three:

1. it intends CCC already, minimum cost is denoted as DP[i][0]
2. it will be influenced by its parent, minimum cost is denoted as DP[i][1]
3. it will influence it’s parent, minimum cost is DP[i][2]

Now, select a root arbitrarily, say it’s 1. We will traverse the whole tree. When we are on node i, we need to calculate the minimum cost required to solve the subtree of node i. So, calculate DP[i][0], DP[i][1],DP[i][2]. Let’s observe the following cases:

1. if Pi=Y or state=1

It denotes i th node is intended directly or indirectly. Now we can pay cost to this node to influence it’s child neighbor node. We have two options here. We can pay or not to pay. Take the minimum value.

2. if Pi=N or state=0 or state=2

It denotes i th node is not intended yet. So, we have to pay at least one of its child to influence its parent node. Which child should we select? at first, we will sum up the cost of all child subtree. If we have several child’s like x1,x2,x3. Calculate the minimum cost for all these child, and take minimum value to influence our parent node as it is not intended. If it is not possible to active the whole tree without paying parent node, just return INT_MAX. Maintain the all these critical cases separately. If you stuck, following code section can be helpful.

Complexity: O(n) where n is the total number of nodes

Code: C++

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mx=3e6+9; 
int n; 
int nrm=0,on=1,pay=2; 
int dp[mx][5];
vector<int> v[mx]; 
string p; 
vector<int>cost; 

int rec(int u, int prev, int state)
{
     int &ret=dp[u][state]; 
     if(ret!=-1) return ret; 
     if(p[u]=='Y' or state==on)
     {
          //try paying
          int ans=cost[u];
          for(auto x: v[u])
          {
               if(x==prev) continue; 
               int cur=rec(x,u,on);
               if(cur==INT_MAX)
               {
                    ans=INT_MAX;
                    break; 
               }
               else ans+=cur; 
          }
          //try without paying
          if(state!=pay)
          {
               int ans1=0; 
               for(auto x: v[u])
               {
                    if(x==prev) continue; 
                    int cur=rec(x,u,nrm);
                    if(cur==INT_MAX)
                    {
                         ans1=INT_MAX; 
                         break; 
                    }
                    else ans1+=cur; 
               }
               ans=min(ans,ans1); 
          }
          return ret=ans; 
     }
     else 
     {
          if((int)v[u].size()==1 and v[u][0]==prev) return ret=INT_MAX; 
          //try paying
          //one child has to pay , rest are on 
          int sum=0; 
          int ans=INT_MAX; 
          for(auto x: v[u])
          {
               if(x==prev) continue; 
               int cur=rec(x,u,on);
               sum+=cur; 
          }
          for(auto x: v[u])
          {
               if(x==prev) continue; 
               int cur1=rec(x,u,on);
               int cur2=rec(x,u,pay);
               if(cur2==INT_MAX) continue; 
               ans=min(ans,sum-cur1+cur2);
          }
          if(ans!=INT_MAX) ans+=cost[u]; 
          //try not paying
          if(state!=pay)
          {
               //one has to pay, rest are normal
               int sum2=0; 
               int ans2=INT_MAX; 
               bool valid=1; 
               for(auto x: v[u])
               {
                    if(x==prev) continue; 
                    int cur=rec(x,u,nrm);
                    if(cur!=INT_MAX) sum2+=cur; 
                    else 
                    {
                         valid=0; break; 
                    }
               }
               if(valid)
               {
                    for(auto x: v[u])
                    {
                         if(x==prev) continue; 
                         int cur1=rec(x,u,nrm);
                         int cur2=rec(x,u,pay);
                         if(cur1==INT_MAX or cur2==INT_MAX) continue; 
                         ans2=min(ans2,sum2-cur1+cur2);
                    }
                    ans=min(ans,ans2);
               }
          }
          return ret=ans;
     }
}

int main()
{
     cin>>n;
     cost.resize(n);
     memset(dp,-1,sizeof dp);
     for(int i=0;i<n-1;i++)
     {
          int a,b; 
          cin>>a>>b; 
          a--; b--; 
          v[a].push_back(b);
          v[b].push_back(a);
     }
     cin>>p; 
     for(int i=0;i<n;i++) cin>>cost[i]; 
     cout<<rec(0,-1,nrm)<<endl; 
}

‍

‍

‍

‍

‍